 oleh Nurul Aifa Fariha Binti Mohd Ruhaizat
oleh Nurul Aifa Fariha Binti Mohd Ruhaizat
STRATEGI : MENGENAL PASTI SUBGOAL
Petak Ajaib

Memahami
masalah
§ membaca
dan memahami soalan dengan teliti serta menyenaraikan maklumat-maklumat yang
terdapat dalam soalan tersebut
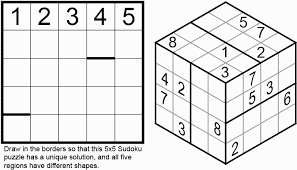
§ menyusun
nombor 1 hingga 9 ke dalam persegi yang dibahagikan kepada 9 segi empat kecil
kuasa dua seperti yang ditunjukkan dalam rajah 1, supaya jumlah lajur setiap
baris dan pepenjuru utama adalah sama (hasilnya adalah sebuah segiempat ajaib).
§ kita
perlu meletakkan setiap sembilan nombor 1,2,3, «« «.., 9 dalam petak kecil,
nombor yang berbeza, supaya jumlah nombor dalam setiap baris dalam setiap
lajur, dan dalam setiap dua pepenjuru yang sama .
§ kenal
pasti adakah jumlah nombor pada setiap ketiga-tiga baris adalah sama.kenalpasti
cara penyelesaian yang sesuai.
Merancang
strategi
§ Membaca
dan memahami soalan dengan teliti serta menyenaraikan maklumat-maklumat yang
terdapat serta merancang strategi yang sesuai untuk digunakan bagi
menyelesaikan masalah tersebut iaitu dengan menggunakan mengenal pasti
‘subgoal’. Strategi ini merupakan satu proses yang mencapai kesimpulan melalui
logik atau pemikiran.
§ Jika
kita tahu jumlah tetap nombor dalam setiap baris, lajur dan pepenjuru, kita
akan mempunyai idea yang lebih baik yang nombor boleh muncul bersama-sama dalam
satu baris tunggal, lajur, atau pepenjuru.
§ Oleh
itu, matlamat subgoal adalah untuk mendapatkan jumlah tetap.
§ Jumlah
sembilan nombor,
§ 1
+2 +3 + «« «. 9, bersamaan dengan 3 kali jumlah dalam satu barisan.
§ jumlah
tetap diperolehi dengan membahagikan 1 +2 +3 + «« «« 9 oleh 3.
§ Seterusnya,kita
perlu memutuskan apakah nombor-nombor yang sesuai untuk diletakkan pada
mana-mana petak. Nombor pada ruang tengah akan muncul dalam 4 jumlah dan
setiapnya ditambah dengan 15.
§ Setiap
nombor di sudut akan muncul dalam tiga jumlah 15.Jika kita menulis 15 sebagai
hasil tambah tiga nombor yang berlainan 1 hingga 9 dalam semua cara yang
mungkin, kita boleh mengira berapa jumlah wang yang mengandungi setiap nombor 1
hingga 9.
§ Nombor-nombor
yang muncul dalam sekurang-kurangnya empat jumlah merupakan calon untuk
penempatan di pusat segi empat, sedangkan nombor yang muncul dalam
sekurang-kurangnya tiga jumlah adalah calon-calon nombor disudut segi empat.
§ Matlamat
baru bagi subgoal adalah untuk menulis 15 dalam sebanyak cara yang mungkin
sebagai hasil tambah 3 nombor yang berbeza dari {1,2,3,…,9}.
Melaksanakan
strategi
§ Masalah
ini boleh diselesaikan dengan menggunakan strategi mengenal pasti subgoal iaitu mengenal pasti matlamat soalan
atau kehendak atau objektif soalan iaitu mendapatkan jumlah tetap.
§ Hasil
tambah 15 boleh ditulis secara sistematik seperti di bawah ini :
9 + 5 + 1 8 + 4 + 3
9 + 4 + 2 7 + 6 + 2
8 + 6 + 1 7 + 5 + 3
8 + 5 + 2 6 + 5 + 4
Menyemak
semula

§ Penyemakan
semula boleh digunakan dengan menggunakan kalkulator.
§ Kita
dapat lihat bahawa 5 adalah satu-satunya nombor di antara nombor yang diberi
yang dapat muncul di tengah-tengah.
§ Satu
lagi cara untuk melihat nombor 5 dapat berada di tengah-tengah adalah dengan
menganggap hasil tambah 1 + 9, 2 + 8, 3 +7, dan 4 +6.
§ Kita
juga dapat tambah 5 untuk mendapatkan 15.